Ⅰ. 서론
통계청이 발표한 2023년 가계금융복지조사 결과를 보면, 우리나라 가계자산에서 실물자산이 차지하는 비중은 76.1%이고, 그것의 93.9%는 부동산자산이다(통계청, 2023). 주택은 가계자산의 가장 중요한 부분이고, 주거의 안정성과 질과 관련되며, 사회적 신분, 자녀 교육, 부와 신분의 세습에도 영향을 미친다. 이 때문에 주택가격의 변동은 이론적으로 또 현실적으로 매우 중요한 연구주제여서 이에 관한 많은 연구가 발표되고 있다(고동우 · 윤성민, 2024; 고희운 · 강상훈, 2023; 윤성민 · 이연정, 2024; 이연정 외, 2023).
주택가격은 주택의 유형, 위치, 크기, 건축연수, 개별적인 특성 등 여러 요인에 따라 제공하는 주거 서비스의 질적 수준에 차이가 크다. 이처럼 주택은 표준화되기 힘든 소비재일 뿐만 아니라, 개인 자산 포트폴리오의 가장 큰 부분을 차지하는 투자 대상이며, 부동산 임대기업의 수익자산이고, 은행 대출에서 빈번히 사용되는 담보이기도 하다. 이렇게 주택이라는 재화의 다양하고 독특한 성격 때문에 수요와 공급에 영향을 미치는 요인들도 특수하다.
주택가격은 주택의 개별적인 특성뿐만 아니라 거시경제 상황과 인구구조 변화에 따라 시간가변적이며 예측하기 힘든 불규칙한 변동을 한다. 주택가격 움직임을 지난 10년 정도만 본다면, 서울, 수도권, 지방 모두에서 주택가격의 움직임은 비슷한 모습을 보인다. 지역별 주택가격은 매우 밀접하게 연결되어 우리나라 주택시장 전체가 하나의 시장처럼 보이기도 한다. 서울 특히 강남지역의 주택가격이 마치 전국 각 지역의 주택가격을 선도하는 소위 ‘강남효과’가 나타난 것 같은 느낌을 주기도 한다. 그렇지만 그보다 다시 10년 정도를 더 거슬러 올라 글로벌 금융위기 전후 10년 동안의 주택가격 움직임을 보면, 각 지역의 주택가격 움직임은 매우 다른 독립적인 모습을 보여준다. 예를 들면, 수도권과 지방의 주택가격이 반대로 움직이는 시기(2008. 10~2013. 9)가 길게 이어진 것을 보면, 이 시기에는 강남효과, 주택시장 동조화, 파급효과 등이 존재하는지 의문이 들기도 한다.
지역별 주택가격 사이의 파급효과 또는 상호의존성은 한 나라 경제의 안정성, 개인들의 투자의사결정, 지역개발 정책, 부동산정책의 정확성 등과 관련된 정부의 정책결정, 사회적 형평성과 인구이동 등을 포함한 여러 다양한 사회문제에 영향을 미치기 때문에 매우 중요한 연구주제이다. 지역별 주택가격 사이의 파급효과는 본 연구의 주제이므로, 이를 좀 더 자세히 살펴보자.
주택시장은 한 경제의 중요한 구성 요소이므로, 지역별 주택시장 사이의 파급효과는 각 지역경제의 변동을 유발하거나 증폭시켜 잠재적으로 광범위한 경제 불안정을 초래할 수 있다. 이러한 현상은 글로벌 금융위기 시기에서와 같이 각 국가의 주택가격 폭락이 이어지는 세계적 차원에서 나타나기도 하지만, COVID-19 시기에서와 같이 우리나라 각 지역의 주택시장이 함께 폭등 및 폭락하는 모습으로 나타나서 경제 불안정을 유발하기도 한다. 주택시장은 금융부문과 밀접하게 연결되어 있어, 파급효과로 인한 주택시장 전반의 불안정은 금융시장 불안정으로 이어질 수도 있다. 2008년 금융위기와 같은 과거의 주택시장 위기는 국지적인 주택문제가 얼마나 광범위한 영향을 미칠 수 있는지를 잘 보여주었다. 부동산 투자자는 투자 결정을 내릴 때 주택가격의 지역별 파급효과를 고려해야 한다. 강남효과와 같이 한 지역의 주택가격이 다른 지역의 주택가격에 영향을 미치면 부동산 투자위험과 수익률을 예측할 때 이러한 파급효과를 중요하게 고려해야만 할 것이다.
주택시장의 지역간 파급효과는 도시 계획과 인프라 개발에도 영향을 미칠 수 있으므로, 지역개발정책 수립에 반영할 필요가 있다. 즉, 한 지역의 주택가격 상승이 인근지역의 주택가격 상승과 지역개발로 이어진다면, 그러한 연계성을 고려하는 보다 총체적이고 미래지향적인 지역개발계획이 수립될 수 있을 것이다. 주택시장의 지역간 파급효과는 지역간 주거 서비스의 경제성 문제를 악화시키거나 완화시켜 사회적 형평성과 각 지역의 인구통계학적 추세에 영향을 미칠 수 있다. 주택가격의 변화는 이주 패턴에 영향을 미칠 수도 있다. 주택정책은 정책 내용뿐만 아니라 정책 타이밍이 중요하다고 알려져 있다. 정책 타이밍이 적절하지 않으면, 문제를 해소하기는커녕 오히려 더 증폭시키는 결과를 낳을 수도 있기 때문이다. 따라서 주택정책 입안자가 효과적인 개입을 설계하려면 지역간 파급효과를 이해하는 것이 중요하다. 특정 지역을 대상으로 한 주택시장 정책이 인근지역 주택가격에 의도하지 않은 결과를 초래할 수도 있으므로, 파급효과를 고려한 조율된 접근 방식이 필요할 수 있다.
이상에서와 같이 주택시장의 지역간 파급효과를 올바르게 이해하면 주택시장뿐만 아니라 주택가격 변동과 관련된 광범위한 사회경제적 영향을 더 잘 이해하고 관리할 수 있을 것이다. 이러한 연구 필요성을 고려하여, 본 연구에서는 우리나라의 가장 중요한 주택시장인 아파트매매시장을 중심으로 지역간 주택가격 파급효과를 분석하려고 한다. 본 연구에서는 표준적인 분석기법뿐만 아니라 선행연구에서 고려하지 못한 시간척도와 시간가변성 문제를 고려하기 위해 소파동 분해(wavelet decomposition) 기법에 기반한 Granger 인과성 검정과 시간가변모수(time-varying parameter, TVP) 연결성지수 네트워크 분석을 이용하여 실증분석을 수행하려고 한다.
본 연구의 구성은 1장의 서론에 이어, 2장에서는 주택시장의 지역간 파급효과와 관련된 선행연구들을 분석한다. 3장에서는 연구대상 표본과 분석방법을 설명하고, 4장에서는 실증분석 결과를 제시하고 설명한다. 5장에서는 본 연구의 주요 결과를 요약하고, 그것의 시사점을 설명한다.
Ⅱ. 선행연구 검토
한 지역의 주택매매가격은 해당 지역 내의 주택수요와 주택공급의 크기에 따라 결정되고 변동한다. 그런데 각 지역 사이에는 인구 이동이 있을 수 있으며 경제활동도 연결되어 있을 수 있어, 주택매매가격의 크기와 변동은 지역간에 연결되어 있을 수 있다. 이러한 생각을 구체화해 Meen(1999)은 중심지역의 주택매매가격의 변동이 인근지역으로 파급되는 확산효과(ripple effect 혹은 spillover effect)의 발생원인을 처음으로 이론적으로 제시하였다. Meen(1999)의 연구 이후 주택가격의 지역간 확산효과에 관한 실증연구들이 이어졌으며, 여러 분석기법이 적용되었다. 특히 VAR(vector autoregressive) 모형, VECM(vector error correction model)을 추정하고 Granger 인과성 검정, 공적분 방정식 추정, 충격반응함수, 예측오차분산분해분석 등의 실증분석 과정을 수행하며 지역별 주택가격 사이의 장기적 균형관계와 단기적 인과관계를 통계적으로 검정하려는 연구들이 다수 발표되었다(Alexander & Barrow, 1994; Ashworth & Parker, 1997; Chiang, 2014; Holmes & Grimes, 2008; Lee & Chien, 2011; Lo et al., 2024; MacDonald & Tylor, 1993; Teye et al., 2017; Tsai, 2015; Xiao, 2023).
한편, Antonakakis et al.(2018)의 연구와 같이 여러 지역 주택가격 사이의 상호 관련성을 Diebold & Yilmaz(2009, 2012, 2014)의 연결성지수(connectedness index)를 측정하여 분석하는 연구들도 다수 발표되었다. Blatt et al.(2023), Chen & Chiang(2020), Chowdhury et al.(2023), Gabauer et al.(2024), Hwang & Suh(2021), Lee & Lee(2019), Tsai(2015, 2022) 등이 이 분석방법을 활용하여 지역별 주택가격 사이의 상호의존성을 분석하였다.
국내 연구도 다수 발표되었는데, 대부분의 연구에서 벡터자기회귀(VAR) 모형 혹은 오차수정모형(VECM)을 이용하는 방법, 혹은 Diebold-Yilmaz의 연결성지수 측정 방법을 활용하고 있다. 먼저, VAR 모형 혹은 VECM을 추정하고, Granger 인과성 검정, 충격반응분석, 예측오차분산분해분석을 이용하는 연구가 다수 발표되었다. 김의준 외(2000)는 수도권 주요 지역 아파트매매가격의 지역간 상호 영향을 분석하였고, 서승환(2007)은 서울과 수도권 주요 지역의 아파트매매가격 통계를 이용하여, 강남구 매매가격 변화가 인접 지역의 매매가격에 영향을 주는 강남효과가 존재한다는 것을 확인하였다. 천인호 · 김진수(2006)는 서울 아파트매매가격 변동이 6대 광역시의 매매가격에 미치는 영향을 분석하였다. VECM 추정결과를 이용한 Granger 인과성 검정결과, 서울 아파트가격은 부산 아파트가격과는 상호 영향을 주고받지만, 다른 광역시 아파트가격에는 일방적인 영향을 준다는 것을 발견하였다. 문규현 · 이동희(2011)는 서울 강남 아파트시장이 전국 또는 인근지역 아파트시장을 선도하고 있다는 것을 확인하였다. 박해선 · 김승년(2014)은 충격반응함수와 예측오차분산분해를 통하여 서울 및 경기지역 아파트매매가격의 지역간 상호의존성을 분석하고, 강남효과를 발견하였다고 보고하였다. 이진숙 외(2017)는 서울 강남과 강북, 6대 도시의 주택매매가격지수 사이의 관계를 Granger 인과성 검정을 이용하여 분석하였다. 김리영(2021)은 충청남도와 충청북도, 대전과 세종시, 그리고 서울과 경기도의 주택가격 사이의 파급효과를 분석하여, 세종시를 포함한 충청권 주택시장은 서울 주택시장과는 독립적인 시장을 형성하고 있다는 것을 밝혔다. 김상배(2023)는 7대 도시 아파트가격 통계를 이용하여 주택가격의 지역간 파급효과를 분석하여, 서울이 다른 지역에 가장 많은 영향을 미치는 것을 발견하였다. 장한익(2023)은 소파동 국면전환 방법을 이용하여 지역별 주택가격 변화 사이의 선후행 관계를 분석하여, 서울 주택시장이 다른 지역 주택가격 변화를 선행하는 경향이 크다는 결과를 보고하였다.
한편, Diebold & Yilmaz(2009, 2012, 2014)가 제시한 연결성지수(connectedness index) 또는 확산효과지수를 측정하고 이를 네트워크로 시각화하여 분석하는 절차의 방법을 이용하는 연구도 다수 발표되었다. 이항용 · 이진(2014)은 7개 대도시 아파트매매가격의 지역간 파급효과를 분석한 결과, 1986~1999년 기간에는 비수도권에서 수도권으로의 파급효과가 더 강하게 나타났지만 2000년 이후에는 수도권에서 비수도권으로의 파급효과가 증가한 것을 발견하였다. 장병기(2014)는 서울, 수도권, 5대 광역시, 지방의 중소도시 지역들 사이의 주택가격 파급효과가 시간이 지남에 따라 감소 추세에 있다는 것을 발견하였다. 박영준 · 김기호(2017)는 수도권 65개의 시 · 구를 8개의 하위지역으로 구분하여 주택가격 파급효과를 분석하였다. 전형철 · 형남원(2018)은 강남 주택시장이 한국 주택시장에서 핵심적인 역할을 하였다고 보고하였다. 박진백 · 홍민구(2019)는 아파트매매가격지수 통계를 이용하여 서울의 5대 생활권역 사이의 주택시장 변동성 파급효과를 확인하였다. 방두완 · 권혁신(2020)은 서울 아파트가격이 대도시 지역에 미치는 영향이 외환위기와 금융위기 기간 이후 점차 감소하는 것을 발견하였다. 정대성 · 박종해(2022)는 경기, 서울, 인천, 부산, 세종, 대전, 충북이 아파트매매시장에서 주도적인 역할을 하는 지역이라고 보고하였다. 정준호(2022)는 수도권 70개 시군구 아파트매매가격의 상승기에는 확산효과 지수가 높아져서 강남효과가 존재하였다는 것을 보여주었다. 고희운 · 강상훈(2023)은 서울과 대도시 아파트매매가격지수를 정상시기, 폭등시기, 폭락시기의 3개로 구분하여 분위별 파급효과를 측정하였다. 이연정 외(2023)는 수도권(서울, 인천)과 지방 광역시 아파트매매가격 변화율 사이의 연계성은 낮다고 보고하였다. 정대성(2023)은 수도권이 비수도권에 비해 파급효과가 강하게 나타나는 것을 발견하였다.
이상에서 보았듯이 여러 지역 주택(혹은 아파트) 가격 사이에 파급효과가 존재하는지를 분석하는 연구가 많이 있지만, 이 연구들은 분석에서 시간척도의 문제를 고려하지 않았다는 공통적인 약점이 있다. 한 지역의 주택가격 변동이 다른 지역으로 파급되기까지는 시간이 걸리게 되는데, 특정 개월 내에 지역별 파급 과정이 완료된다고 가정하는 것은 부적절하다고 생각된다. 이러한 비현실적인 가정 문제를 피하기 위해서는 본 연구에서와 같이 시간척도(단기, 중기, 장기)를 달리하며 파급효과를 분석하는 것이 옳을 것이다. 또한 Diebold-Yilmaz가 제시한 연결성지수를 측정하여 분석하는 방법은 지역들 사이 연결성의 전체적인 모습을 네트워크화하여 한눈에 파악할 수 있게 한다는 장점이 있지만, 연결된 인과관계를 파악할 수 있는 어떤 통계적 검정을 수행하는 것이 아니어서 지역별 주택가격 사이의 관계에 대한 엄밀한 증거를 제시하는 것은 아니다(Xiao & Huang, 2018). 이러한 약점은 Granger 인과성 검정과 같은 인과관계에 대한 통계적 검정을 추가 수행하여 보완될 필요가 있다. 선행연구에서의 이러한 문제를 완화하기 위해 본 연구에서는 소파동 분해 기법을 이용하여 주택가격 움직임을 시간척도별로 분해하고, 단기, 중기, 장기 시간척도별로 Granger 인과성 검정을 수행하려고 한다. 그리고 표준적인 Diebold-Yilmaz 연결성지수 네트워크의 약점을 보완하기 위해 개발된 시간가변모수(time-varying parameter) VAR 모형을 이용한 TVP-VAR(time-varying parameter vector autoregressions) 연결성지수 네트워크를 구성하여 자의적인 모형설정을 피하고 풍부한 분석결과를 얻으려고 한다.
Ⅲ. 표본자료 및 분석방법
주택시장은 주택의 유형(아파트, 단독주택, 연립주택)에 따라 구분되어 있지만, 본 연구에서는 그 중에서 상대적으로 표준화의 정도가 높고 거래규모가 가장 큰 시장인 아파트매매시장을 분석대상으로 선택하려고 한다. 그리고 지역 주택시장은 서울(전체, 강북지역, 강남지역으로 구분하여 분석), 수도권, 6개 지방 광역시의 아파트매매시장을 선택하여, 1986년 1월부터 2023년 12월까지의 월별 아파트매매가격지수 사이의 파급효과를 분석하기로 한다. 이 통계는 KB국민은행에서 발표하는 월간 주택가격동향(https://data.kbland.kr)에서 수집하였다.
그런데 주택가격의 변동 중에서는 인플레이션 때문에 발생하는 부분이 있으므로, 파급효과를 올바르게 파악하기 위해서는 그 부분을 제외하는 것이 적절할 것이다. 이를 위하여 본 연구에서는 실질 아파트매매가격을 표본으로 설정하려고 한다. 실질 매매가격지수는 명목 매매가격지수를 소비자물가지수로 나누어 계산하였고, 소비자물가지수는 KOSIS 국가통계 포털(https://kosis.kr)에서 구하였다. 월별 자료는 계절적 영향을 많이 받으므로, 그 영향을 제거하기 위해 모든 자료는 X-11 방법으로 계절조정을 한 다음에 사용하였다.
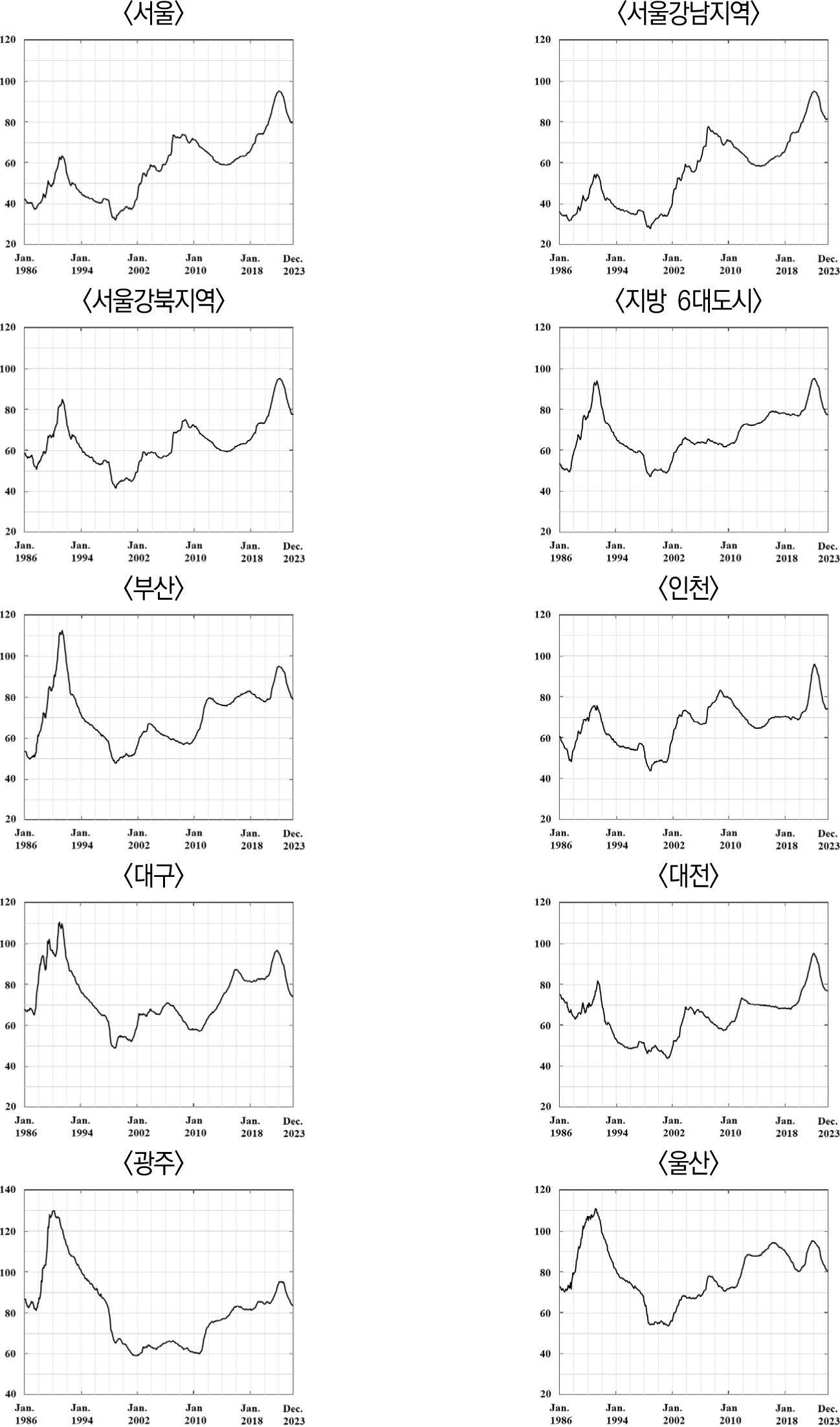
실증분석에 이용된 통계의 움직임은 <그림 1>과 같다. 그림들에서 볼 수 있듯이, 1986년 중반부터 소위 ‘3저 호황(저금리, 저유가, 저달러)’ 시기에 연 12% 수준의 고도성장이 이어지고 사상 최초의 무역수지 흑자로 유동성이 매우 풍부하여 주식시장은 물론 아파트시장의 폭등이 나타난다. 서울과 지방 대도시 등 모든 지역의 주택시장에서 아파트매매가격이 크게 상승한다. 이러한 아파트가격 폭등은 대체로 1991년 중반까지 3년 정도 이어지지만, 상승 기간과 상승 정도에는 지역별 차이가 있다는 것을 볼 수 있다.
1992년 이후 10년간은 아파트 실질매매가격이 폭락하였으며, 2000년 이후 약 20년간 아파트매매가격은 지역별로 상당히 다른 패턴을 보인다. 서울 아파트시장은 상승-하락-상승의 움직임을 보였지만, 부산과 울산 아파트시장은 작은 변동을 보이면서도 추세적으로 상승하는 움직임을 보였고, 광주는 정체 이후 상승하는 움직임을 보였다. 각 지역의 아파트시장은 여러 차례 등락을 반복하였지만, 전체적으로 실질가격이 상승하였다. 그렇지만 2020년부터는 COVID-19 이후 풍부한 유동성에 힘입어 아파트 실질가격이 급등하지만 이러한 상승 흐름이 오래 이어지지는 못하고, 2022년 이후에는 급락하여 대체로 COVID-19 이전 가격수준으로 되돌아가는 모습을 보인다. 특히, 대구와 광주의 아파트시장은 최근 실질매매가격이 COVID-19 이전보다도 더 낮은 수준으로 하락하는 움직임을 보인다.
<표 1>은 실증분석에 사용된 변수들의 기초통계량을 요약하였다. 표에서 가장 우측에 요약된 아파트 실질가격 변화율(%) 부분을 보면, 전월대비 가격변화율의 전국 평균은 0.09%인데, 지역별 변화율이 이보다 높은 지역은 서울강남지역(0.18%)이 유일하다. 서울강북지역(0.06%)은 강남지역과는 큰 차이를 보이고 있으며, 전국 광역시 평균(0.08%)보다도 더 낮다는 것을 알 수 있다. 광역시 중에는 부산(0.09%)의 변화율이 높아 전국 평균 정도이지만, 광주(-0.01%)는 오히려 하락한 것으로 나타났다. 전체적으로 보면, 각 지역별 변화율의 차이가 매우 크다는 것을 알 수 있다. 표본기간 중 서울강남지역의 아파트가격 상승률이 가장 높게 나타났지만, 그 사실이 강남지역이 타지역에 파급효과를 유발한다는 것을 의미하지는 않는다.
한편, 변화율의 표준편차(SD)의 값을 보면, 서울(특히 강남지역)의 표준편차가 크게 나타나 서울의 아파트가격 변동이 심했다는 것을 알 수 있다. 지방 대도시들의 표준편차도 대부분 전국 평균(1.01%)보다 높게 나타났으며, 특히 대구(1.31%), 부산(1.22%), 인천(1.20%)의 표준편차가 높게 나타났다. 이러한 사실은 대도시 지역의 아파트가격 변동이 전국 평균보다 더 심하였다는 것을 의미한다. 그렇지만, 아파트가격 변동의 정도가 지역별로 차이가 크다는 것도 알 수 있다.
<표 2>에는 세 가지 시계열에 대한 단위근 검정 결과들이 요약되어 있다. 이 표의 첫 번째 열은 수준변수(지역별 아파트 실질매매가격지수) 시계열에 대한 검정인데, 수준변수 시계열은 비정상(nonstationary) 시계열이라는 것을 알 수 있다. 두 번째 열에는 로그 수준변수 시계열에 대한 검정결과들인데, 모든 지역 경우에서 역시 비정상 시계열로 나타났다. 세 번째 열은 변화율 시계열에 대한 단위근 검정 결과들인데, 모든 지역 경우에서 정상 시계열인 것으로 나타났다. 따라서 이후의 실증분석은 이러한 단위근 검정결과에 기초하여 변화율 변수를 이용하여 진행하기로 한다.
소파동 변환(wavelet transformation, WT)은 시간흐름 영역과 시간척도(빈도, 주파수) 영역 모두에서 시계열의 움직임을 분석하기 위해 사용하는 기법이다. 소파동 변환기법은 연속적 소파동 변환(continuous wavelet transformation, CWT)과 이산적 소파동 변환(discrete wavelet transformation, DWT)으로 구분된다. DWT는 시계열 움직임에 포함된 소음을 줄이거나 데이터 정보압축 분야에서 많이 사용되는데, 본 연구에서는 연구대상 시계열로부터 시간척도별로 분해한 시계열을 얻기 위해 DWT 기법을 이용하려고 한다.
소파동 분석은 모 소파동 함수(mother wavelet function)라고 불리는 기저함수(basis function)를 이용하여 시간 영역과 주파수(시간척도, 빈도) 영역에서의 특성을 함께 추출하여 보여준다(Genҫay et al., 2002; Percival & Walden, 2000). 모 소파동 함수 Ψ(ω)에서 도출되는 자 소파동 함수(child wavelet function) Ψu,s (t)을 이용하여 t 시점에서 분석대상 시계열 x(t)를 분해하면 해당 시계열에 포함된 시간-주파수 영역의 정보를 추출할 수 있다. Grinsted et al.(2004)와 Torrence & Compo(1998)에서 사용한 표기법으로 소파동 함수를 다음과 같이 나타낼 수 있다.
여기서 u는 시간위치(혹은 시간이동의 크기)를 조정하는 모수(location parameter)이고, s는 진동의 지속기간을 늘리거나 줄이는 역할을 하는 척도모수(scale parameter)이다. 시간척도 s가 큰 경우는 낮은 주파수의 진동을 묘사하는데, 이는 소파동 시계열의 진폭(amplitude)이 크고 주기가 길다는 것을 의미한다.
소파동 분석에는 여러 가지 유형의 모 소파동이 활용되고 있는데, 그 각각은 특성이 달라 서로 다른 목적을 위해 사용된다. 진폭과 위상(phase)에 관한 시계열 정보분석에서는 Morlet 소파동이 좋은 선택이라고 알려져 있으므로(Percival & Walden, 2000), 본 연구에서도 아래의 Morlet 소파동 함수를 이용하기로 한다.
여기서 ω0는 소파동의 중심 주파수인데, ω0의 값에 대한 선택은 시간과 주파수의 균형을 조절해 준다. 본 연구에서는 Grinsted et al.(2004)과 Rua & Nunes(2012)를 참고하여 ω0=6으로 설정한다.
l번째 시간척도에 대응되는 분해된 시계열을 Dl로 표시하고, 각 시간척도에서의 변동의 누적합인 평탄화계수(smooth coefficients)를 Sl로 표시하면, 연구대상 시계열은 다음과 같이 분해된 시계열의 합으로 나타낼 수 있다(Gençay et al., 2002).
본 연구에서는 Gençay et al.(2002)이 제안한 비대칭적 소파동 필터를 이용하여 연구대상 시계열을 분해하며, 표본수를 고려하여 L=5로 설정한다. 그리고 단기주기 시계열은 (D1+D2)/2, 중기주기 시계열은 (D3+D4)/2, 장기주기 시계열은 (D5+S5)/2로 정의하여 계산하고, 각 주기별 시계열을 실증분석에 이용하기로 한다.1)
지역별 주택매매가격 변화율 사이의 동적 연결성을 측정하기 위해, 본 연구에서는 Antonakakis & Gabauer(2017)의 TVP-VAR 연결성지수를 이용하려고 한다. 이 지수는 Diebold & Yilmaz(2012) 방법을 Koop & Korobilis(2014)가 제안한 TVP-VAR 모형을 이용하여 확장한 것인데, 분산-공분산 행렬이 시간 흐름에 따라 변화할 수 있도록 한 일반화된 지수이다. TVP-VAR 연결성지수는 변수 사이의 관계가 시간가변적이라는 현실을 반영하고 있고, 표본을 모두 이용할 수 있고, 저빈도자료에서도 적용할 수 있고, 이동표본창(rolling window)의 크기를 임의로 선택해야 하는 문제를 피할 수 있다는 장점이 있다(Antonakakis et al., 2020).
Antonakakis & Gabauer(2017)의 연결성지수 측정방법은 Koop & Korobilis(2014)가 제안한 다음의 TVP-VAR(p) 모형 추정치를 이용한다.
여기서 rt는 (K×1) 차원의 연구대상 시계열(지역별 아파트매매가격 변화율) 벡터, zt-1=[rt-1, …, rt-p]′는 (Kp×1) 차원 벡터, Bt는 (K×Kp) 차원의 시간가변 모수 행렬, εt는 (K×1) 차원의 백색잡음 오차항 벡터이며, (K×K) 차원의 시간가변 분산-공분산 행렬 St를 가진다. ve c(Bt)는 Bt 를 벡터화(vectorization)한 (K2p×1) 차원의 벡터, vt는 (K2p×1) 차원의 벡터, Rt는 (K2p×K2p) 차원의 행렬이다. Ωt-1 는 (t-1)기에 이용할 수 있는 모든 정보의 집합을 나타낸다.
Wold(1948) 정리를 이용하면, TVP-VAR은 다음과 같은 TVP-VMA(vector moving average) 모형으로 변환될 수 있다. , A0=IK, . 여기서 Ah,t는 (K×K) 행렬인데, 이 추정치를 이용하여 일반화 충격반응함수(generalized impulse response functions, GIRF)와 일반화 예측오차분산분해(generalized forecast error variance decomposition, GFEVD)를 측정할 수 있다(Koop et al., 1996; Pesaran & Shin, 1998).
GIRF(Ψij,t (H))는 H 기간 후를 예측할 때 i 변수의 충격에 따른 다른 모든 j 변수의 반응을 나타내며, Gabauer & Gupta(2018)의 제안에 따라 다음과 같이 추정될 수 있다.
그리고 GFEVD (φ̃ij,t (H))는 Koop et al.(1996)의 제안에 따라 다음과 같이 계산된다.
이렇게 계산된 GFEVD 를 이용하여 여러 연결성지수들을 측정할 수 있다. 먼저, 총연결성지수(total connectedness index, TCI)는 다음과 같이 측정될 수 있다.
또, 다른 모든 변수들(j)로부터의 충격으로부터 특정 시장(i)이 받은 반응을 측정하기 위한 방향성 연결성지수(FROM)는 다음과 같이 나타낼 수 있다.
그리고 특정 변수(i)에서 발생한 충격이 다른 모든 변수들(j)에게 전달된 정도를 측정하기 위한 방향성 연결성지수(TO)는 다음과 같이 나타낼 수 있다.
또 이들을 이용하여 아래와 같이 순연결성지수(net connectedness index, NET)를 정의할 수 있는데, 이는 특정 i 변수로부터 다른 모든 j 변수들에 전달된 순연결성의 정도를 측정하기 위한 것이다.
NETi 〉0이면, i 변수는 연구대상 변수들의 네트워크를 주도적으로 움직이는 정보 전달자(transmitter)의 역할을 한다는 것을 의미한다. 반대로 NETi 〈0이면, 해당 변수는 네트워크 내의 다른 변수들로부터 영향을 받는 정보 수령자(receiver)의 역할을 하는 것을 의미한다.
두 변수 사이의 인과관계를 알아보는 연구에 사용되는 가장 보편적인 방법은 Granger(1969) 인과성 검정이다. Granger(1988)는 다음의 조건이 만족되면 변수 x는 변수 y를 Granger 인과한다고 정의한다.
다음의 조건이 만족되면 변수 x는 변수 y를 Granger 인과하지 않는다고 정의한다.
Ⅳ. 실증분석결과 및 해석
앞에서 설명한 연결성지수를 측정하기 위해서는 먼저 연결된 네트워크에 포함시킬 지역별 아파트매매시장을 선택하여야 한다. <표 3>에는 지방 대도시의 6개 아파트매매시장과 서울전체 시장으로 네트워크를 구성하여, TO, FROM, NET 연결성지수를 측정한 결과를 요약하였다. 이 표를 보면 네트워크 내에서 가장 큰 영향을 미치는 지역별 시장은 서울 아파트시장인 것을 알 수 있다. 서울 시장은 타지역 시장으로부터 영향을 비교적 적게 받아, NET가 양수의 큰 값으로 측정되었다. 이러한 결과는 서울 아파트매매시장이 네트워크 내에서 가장 강력한 정보 전달자의 역할을 한다는 것을 나타내며, ‘서울효과’가 존재한다고 말해도 된다는 것을 의미한다.
| 서울 | 부산 | 인천 | 대구 | 대전 | 광주 | 울산 | TCI | |
|---|---|---|---|---|---|---|---|---|
| TO | 89.91 | 65.41 | 48.16 | 68.30 | 40.40 | 41.37 | 40.52 | 56.3% |
| FROM | 53.82 | 62.07 | 61.90 | 58.62 | 41.67 | 58.13 | 57.86 | |
| NET | 36.09 | 3.34 | -13.74 | 9.68 | -1.27 | -16.76 | -17.34 |
대구와 부산 아파트시장의 NET도 양수의 값으로 측정되어, 이 두 시장도 타지역 아파트시장으로부터 영향을 받는 것보다 영향을 주는 부분이 더 큰 정보 전달자의 역할을 하는 것으로 나타났다. 반면, 울산, 광주, 인천 아파트시장은 NET가 음수의 값으로 측정되어, 이 세 시장은 타지역 아파트시장에 영향을 주는 것보다 영향을 받는 부분이 더 큰 정보 수령자의 역할을 하는 것으로 나타났다. 대전 아파트시장의 경우는 타지역 시장에 영향을 적게 주고 적게 받는 상대적으로 독립적인 움직임을 보이는 시장으로 나타났다.
<표 4>에는 서울 전체시장 대신에 서울강 남지역 아파트매매시장이 포함된 네트워크에서 연결성지수들을 측정한 결과를 요약하였다. 이 표에서도 서울강남지역, 대구, 부산 아파트시장은 정보 전달자의 역할을 하고 있고, 울산, 광주, 인천은 정보 수령자의 역할을 하고 있으며, 대전 아파트시장의 경우는 타지역 시장에 비해 상대적으로 독립적인 움직임을 보이는 시장으로 나타나는 부분은 대체로 유사하다. 이 네트워크 내에서도 서울강남지역의 영향력은 단연 강하게 나타나므로, ‘강남효과’가 실제로 존재한다고 볼 수 있을 것 같다.
| 서울강남 | 부산 | 인천 | 대구 | 대전 | 광주 | 울산 | TCI | |
|---|---|---|---|---|---|---|---|---|
| TO | 85.14 | 65.52 | 46.06 | 68.92 | 40.70 | 41.16 | 39.71 | 55.3% |
| FROM | 50.86 | 61.48 | 60.49 | 58.28 | 41.24 | 57.50 | 57.37 | |
| NET | 34.28 | 4.04 | -14.42 | 10.65 | -0.54 | -16.34 | -17.66 |
<표 5>에는 서울강북지역 아파트매매시장이 포함된 네트워크에서 연결성지수들을 측정한 결과를 요약하였다. 이 표에서도 서울강북지역, 대구, 부산 아파트시장은 정보 전달자의 역할을 하고 있고, 광주, 울산, 인천은 정보 수령자의 역할을 하고 있으며, 대전 아파트시장의 경우는 타지역 시장에 비해 상대적으로 독립적인 움직임을 보이는 시장으로 나타나는 부분은 대체로 유사하다. 그렇지만 서울강북지역의 네트워크 내에서의 영향력은 서울강남지역에 비해 크게 약하다는 것을 알 수 있다.
| 서울강북 | 부산 | 인천 | 대구 | 대전 | 광주 | 울산 | TCI | |
|---|---|---|---|---|---|---|---|---|
| TO | 76.24 | 70.72 | 57.13 | 70.13 | 40.71 | 38.14 | 42.38 | 56.5% |
| FROM | 57.49 | 61.11 | 60.50 | 58.15 | 42.52 | 57.85 | 57.82 | |
| NET | 18.74 | 9.61 | -3.37 | 11.97 | -1.81 | -19.71 | -15.44 |
한편 총연결성(TCI)의 정도는 어느 네트워크에서 측정하든지 대체로 유사하게 나타났다. 그런데 <표 3>~<표 5>의 측정결과는 모두 각각의 시점에서 계산된 연결성지수의 평균값이어서 전체 기간에서 연결성지수들의 동적 움직임을 알 수 없다는 한계가 있다. 이러한 약점은 연결성지수의 평균값 대신 그것들의 동적 움직임을 살펴보면 해소될 수 있다. 이제부터 각 연결성지수의 움직임을 다음 그림을 통해 파악해보기로 하자.
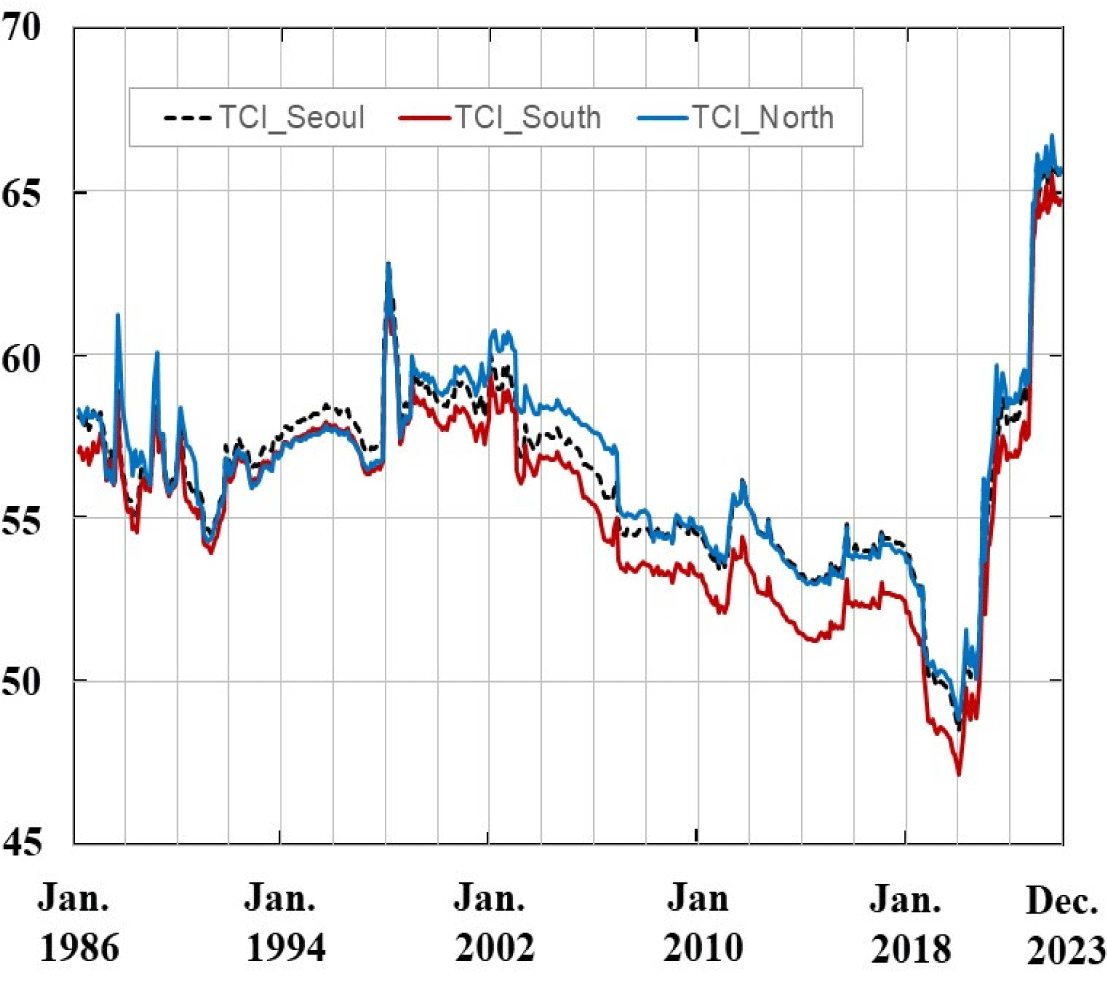
<그림 2>에 나타낸 총연결성지수(TCI)의 움직임을 보면, 세 가지 기준의 TCI 모두 시간에 따라 가변적이며 경제상황에 따라 달라진다는 것을 알 수 있다. 그렇지만 세 가지 기준의 지수의 전체적인 움직임은 대동소이하다는 것을 볼 수 있다. 대체로 2000년대 초반부터 TCI는 감소하는 것으로 나타나는데, 이는 지역간 아파트가격 움직임의 동조화가 그 이전 시기보다 약해졌다는 것을 의미한다. 그렇지만 COVID-19 팬데믹 초기인 2020~2021년 아파트가격 상승시기에는 지역 사이의 동조화가 크게 증가하는 것을 볼 수 있다. 이어진 2022~2023년 아파트가격 하락시기에 지역별 동조화가 더 심해진 것을 볼 수 있다. 이 사례는 지역별 아파트가격 동조화가 상승시기뿐만 아니라 하락시기에도 나타날 수 있고, 가격 급등 및 급락 시기에 크게 강화된다는 것을 보여준다.
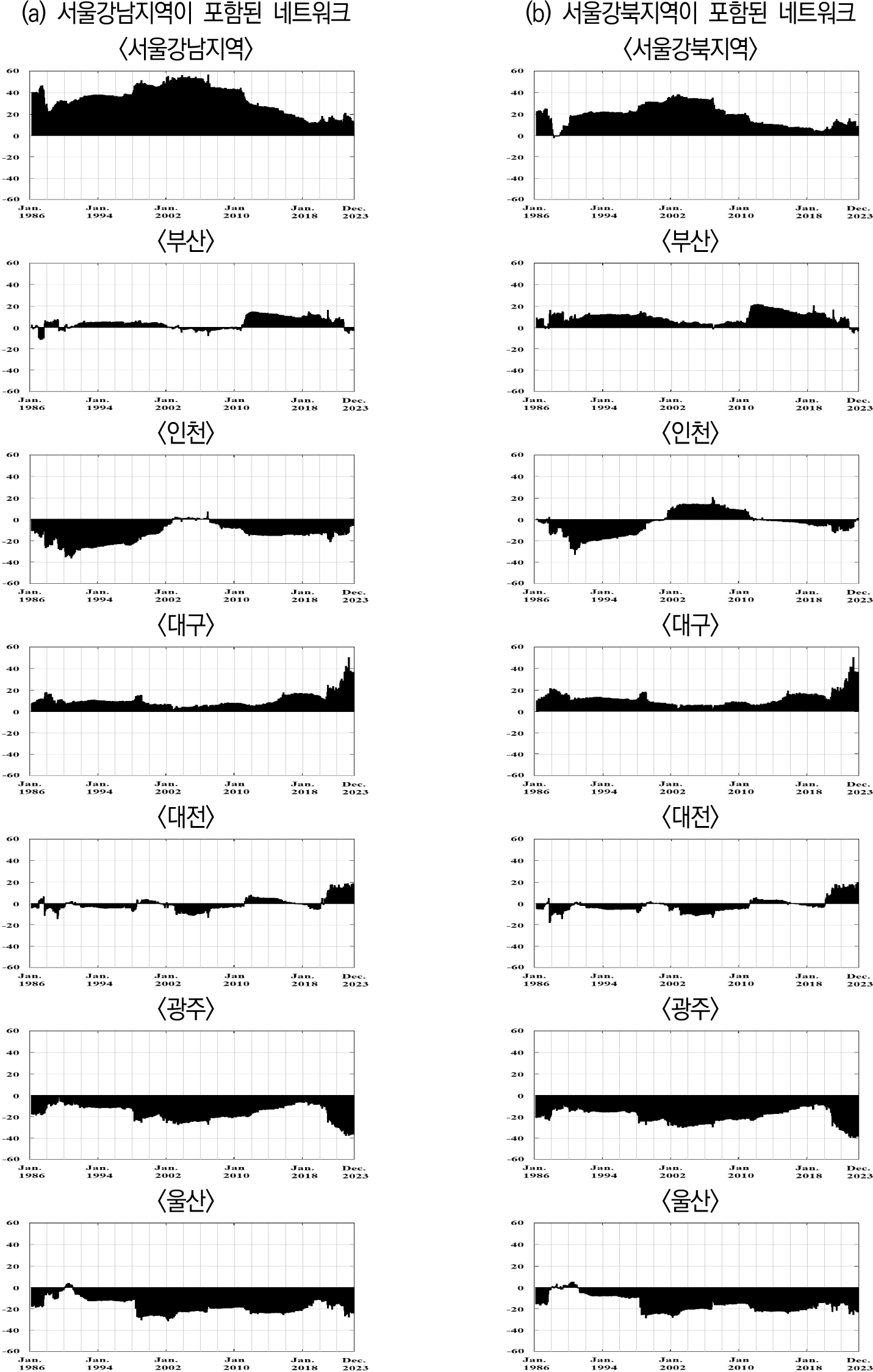
<그림 3>에는 두 가지 네트워크(지방 6대도시에 서울강남지역과 서울강북지역이 각각 포함된 네트워크)에서 계산한 순연결성지수(NET)의 움직임을 보여주고 있다. NET 지수는 해당 변수가 다른 모든 변수에 미친 영향에서 다른 모든 변수의 충격으로부터 받은 영향을 뺀 값이다. 그림에서 서울강남지역과 서울강북지역의 NET는 어느 시검에서 측정하더라도 모두 양수의 값으로 나타난다. 이는 이 두 지역의 아파트매매가격 변화율이 두 네트워크를 움직이는 정보 전달자의 역할을 하는 것을 나타낸다. 즉, 서울강남지역과 서울강북지역의 아파트매매가격은 지방 6대도시 아파트매매시장을 선도하는 것을 의미한다. 특히 서울강남지역의 NET 값이 강북지역보다 더 큰 양수의 값으로 나타나므로 강남효과가 강북효과보다 더 강하다는 것을 알 수 있다. 그렇지만 이러한 서울 아파트매매시장의 영향력은 2010년 이후에는 크게 약화되고 있는 것을 알 수 있다.
2010년 이후에는 부산과 대구의 NET 값이 양수로 나타나며, 특히 대구의 경우 COVID-19 이후 시기에 NET의 양수 값이 크게 증가한 것을 볼 수 있다. COVID-19 이후 시기에는 강남효과나 강북효과 등 서울효과보다 대구효과가 더 크게 나타나고 있는데, 이러한 결과는 대구가 가장 강력한 아파트매매시장 정보 전달자의 역할을 하며 전국 아파트매매시장 움직임을 선도하고 있는 것을 의미한다.
한편, 광주와 울산은 측정 시점과 무관하게 대체로 NET 값이 음수로 측정되고 있는데, 이러한 결과는 이 두 지역의 아파트매매시장이 다른 지역의 아파트매매시장으로부터 영향을 받는 정보 수령자의 역할을 하는 것을 나타낸다. 즉, 광주와 울산의 아파트매매시장은 다른 지역 아파트매매시장의 움직임으로부터 주로 영향을 받는 시장이라는 것을 의미한다.
인천과 대전의 경우는 시기에 따라 양수와 음수의 값이 바뀌면서 한동안 이어지는 모습을 보여주고 있다. 이러한 결과는 이 두 지역 아파트매매시장의 역할이 일정하지 않고 시기에 따라 달라지는 것을 의미한다. COVID-19 이후 시기에는 인천은 정보 수령자, 대전은 정보 전달자의 역할을 하는 것을 알 수 있다.
앞에서 살펴본 표와 그림의 결과들은 전체적인 상황을 일목요연하게 한눈에 파악할 수 있다는 장점이 있지만, 통계적 분석을 수행한 것은 아니어서 아쉬움이 있다. 그리고 시장참가자의 투자시야(시간척도, 주파수)를 고려하지 않아 시간척도별로 나타날 수 있는 차이를 파악하지 못한다는 약점도 있다. 이러한 부분을 보완하기 위해, 이제부터는 원래의 시계열을 소파동 기법을 이용하여 시간척도(단기, 중기, 장기)에 따라 분해하고, 각 시간척도별로 분해된 시계열을 이용하여 Granger 인과성 검정을 수행하였다. 그 결과는 <표 6>~<표 8>에 요약되어 있다.
<표 6>에는 단기 시간척도의 시계열을 이용하여 수행한 Granger 인과성 검정의 결과를 요약하였는데, 이 표의 윗부분에는 서울 전체 아파트매매시장과 타지역 아파트매매시장 사이의 인과성을 검정한 결과가 표시되어 있다. 5% 유의수준을 기준으로 한다면, 서울 아파트시장은 지방 6대도시 시장에 영향을 미치는 것으로 나타났다. 그렇지만, 부산, 광주, 울산의 아파트시장도 서울 전체 아파트시장에 영향을 미치는 양방향의 인과관계가 존재하는 것으로 나타났다. 인천, 대구, 대전 아파트시장은 서울 전체 아파트시장에 유의한 영향을 미치지 못하는 것으로 나타났다. 따라서 인천, 대구, 대전의 관점에서 본다면, 아파트가격의 서울효과가 존재한다고 볼 수 있다. 그렇지만, 부산, 광주, 울산의 관점에서 본다면, 서울과 상호 영향을 미치는 관계이지 서울효과라고 말할 수 없다는 것을 알 수 있다.
이 표의 중간 부분에는 서울강남지역 아파트매매시장과 타지역 아파트매매시장 사이의 인과성을 검정한 결과가 표시되어 있다. 5% 유의수준을 기준으로 한다면, 서울강남지역 아파트시장은 지방 6대도시 시장에 유의한 영향을 미치는 것으로 나타났다. 그렇지만, 부산, 인천, 광주, 울산의 아파트시장도 서울강남지역 아파트시장에 영향을 미치는 양방향의 인과관계가 존재하는 것으로 나타났다. 대구, 대전 아파트시장은 서울강남 아파트시장에 유의한 영향을 미치지 못하는 것으로 나타났다. 따라서 대구, 대전의 관점에서 본다면 아파트가격의 강남효과가 존재한다고 볼 수 있지만, 부산, 인천, 광주, 울산의 관점에서 본다면 서울강남지역과 상호 영향을 미치는 관계이지 강남효과라고 부를 수 없다는 것을 알 수 있다.
이 표의 아랫부분에는 서울강북지역 아파트매매시장과 타지역 아파트매매시장 사이의 인과성을 검정한 결과가 표시되어 있다. 5% 유의수준을 기준으로 한다면, 서울강북지역 아파트시장은 지방 대도시 시장에 유의한 영향을 미치지만 부산 시장에는 유의한 영향을 미치지는 못하는 것으로 나타났다. 그렇지만, 인천과 울산의 아파트시장도 서울강북지역 아파트시장에 영향을 미치는 양방향의 인과관계가 존재하는 것으로 나타났다. 부산, 대구, 대전, 광주 아파트시장은 서울강북 아파트시장에 유의한 영향을 미치지 못하는 것으로 나타났다. 따라서 대구, 대전, 광주의 관점에서 본다면 아파트가격의 강북효과가 존재한다고 볼 수 있지만, 부산, 인천, 울산의 관점에서 본다면 강북효과가 존재하지 않는다는 것을 알 수 있다.
<표 7>에는 중기 시간척도의 시계열을 이용하여 수행한 Granger 인과성 검정의 결과를 요약하였는데, 이 표의 윗부분을 보면 서울 전체 아파트시장은 지방 6대도시 시장에 영향을 미치는 것으로 나타났다. 부산, 대구, 대전의 관점에서는 서울효과가 존재한다고 볼 수 있지만, 인천, 광주, 울산의 관점에서는 양방향의 상호관계가 존재하는 것으로 나타났다. 이 표의 중간 부분을 보면, 강남효과는 대구의 관점에서만 존재하고, 부산, 인천, 광주, 울산의 관점에서는 상호 영향을 주고받는 관계가 존재하는 것을 알 수 있다. 이 표의 아랫부분을 보면, 대구, 울산의 관점에서만 강북효과가 존재하고 부산, 대전, 광주의 관점에서는 양방향의 인과관계가 존재하는 것으로 나타났다.
<표 8>에는 중기 시간척도의 시계열을 이용하여 수행한 Granger 인과성 검정의 결과를 요약하였는데, 이 표의 윗부분을 보면, 서울 전체와 6대 지방대도시 아파트매매시장 사이에는 양방향의 인과관계가 존재하므로 서울효과라고 부를 만한 현상이 나타나지 않았다는 것을 알 수 있다. 이 표의 중간 부분과 아랫부분을 보더라도 강남효과나 강북효과가 존재하는 것이 아니라 양방향의 상호관계가 존재하는 것을 알 수 있다.
이 표들에서의 결과를 전체적으로 살펴보면 다음과 같다. 첫째, 서울효과, 강남효과, 강북효과는 일부 지방도시의 관점에서만 존재하는 것이고 모든 지방대도시의 관점에서 나타나는 현상은 아니며, 상호 영향을 미치는 양방향 인과관계가 존재하는 예도 빈번하게 나타났다. 둘째, 서울효과, 강남효과, 강북효과는 단기 시간척도 시계열에서 상대적으로 빈번하게 나타나지만, 장기 시간척도에서는 그런 효과는 존재하지 않았다. 장기 시간척도에서는 양방향의 상호 인과관계가 일반적으로 존재하는 것으로 나타난다.
Ⅴ. 결론
본 연구에서는 우리나라 주택시장의 지역간 파급효과를 거래가 많고 상대적으로 표준화의 정도가 높은 아파트매매시장을 중심으로 살펴보았다. 연구대상에 포함된 지역 주택시장은 서울(전체, 강북지역과 강남지역으로 구분하여 분석), 6개 지방 광역시의 아파트매매시장이며, 1986년 1월부터 2023년 12월까지의 월별 아파트매매가격지수 사이의 파급효과를 분석하였다. 본 연구에서는 지역별 아파트시장 연결성의 전체적인 모습을 파악하기 위한 시간가변모수 연결성 네트워크 기법, 시간척도와 시간가변성 문제를 고려하기 위한 소파동 분해 기법, 통계적 검정을 위한 Granger 인과성 검정 기법을 이용하여 실증분석을 수행하였다.
본 연구에서 얻은 주요 결과를 요약하면 다음과 같다. 첫째, 지역별 아파트매매시장 네트워크의 총연결성지수(TCI)의 움직임을 보면, 대체로 2000년대 초반부터 지역간 아파트가격 움직임의 동조화가 그 이전 시기보다 약해졌지만, COVID-19 팬데믹 초기인 2020~2021년 아파트가격 상승시기와 2022~2023년 아파트가격 하락시기에 지역별 아파트매매가격 동조화가 강해진 것을 발견하였다. 둘째, 지역별 순연결성지수(NET)를 측정하여 본 결과, 대체로 서울 전체, 강남지역, 강북지역은 네트워크 내에서 가장 강력한 정보 전달자의 역할을 하는 것으로 나타났으며, 특히 강북지역보다 강남지역의 영향력이 훨씬 더 강하게 나타났다. 그렇지만 이러한 서울 아파트매매시장의 영향력은 2010년 이후에는 크게 약화되고 있는 것으로 나타났다. 대구와 부산 아파트시장도 정보 전달자의 역할을 하고, 울산, 광주, 인천 아파트시장은 정보 수령자의 역할을 하며, 대전 아파트시장은 상대적으로 독립적인 움직임을 보이는 시장임을 발견하였다. 셋째, 시간척도별 Granger 검정 결과로부터 서울효과, 강남효과, 강북효과는 일부 지방도시의 관점에서만 존재하는 것이고 모든 지방대도시의 관점에서 나타나는 현상은 아니며, 단기 시간척도 시계열에서 상대적으로 빈번하게 나타나는 현상이라는 것을 알 수 있었다. 장기 시간척도에서는 그런 효과는 존재하지 않으며, 장기 시간척도에서는 양방향의 상호 인과관계가 일반적으로 존재하는 것으로 나타났다.
이상의 분석결과는 정부의 아파트매매시장 가격안정화 정책이 지역별 특성을 고려하여 수립될 필요가 있다는 것을 시사한다. 특히 정보 전달자의 역할을 하는 지역과 정보 수령자의 역할을 하는 지역에 대한 정책을 구분하여 수립할 필요가 있다. 그리고 아파트시장 안정화정책 담당자가 어떤 시야를 가지고 아파트매매가격 정책을 수립하는가는 매우 중요한 부분이다. 단기 시간척도에서 보면, 서울지역(전체, 강남, 강북)은 전국의 아파트시장에 미치는 영향이 강하므로, 우선적인 정책 대상 지역이 되어야 한다. 특정 지역을 대상으로 한 주택시장 정책이 인근지역에 의도하지 않은 결과를 초래할 수도 있으므로, 파급효과를 고려한 조율된 접근 방식이 필요할 수 있다. 그렇지만, 장기 시간척도에서 보면, 서울지역과 지방대도시 아파트시장 사이에는 양방향의 인과관계가 있으므로 그러한 피드백(feedback) 효과를 정책수립에 고려할 필요가 있다. 그리고 시간척도의 중요성을 이해할 필요가 있으며, 이 측면을 이해하지 못하면 문제를 해소하기는커녕 오히려 더 증폭시키는 결과를 낳을 수도 있다. 장기 시간척도 관점에서의 서울-지방 시장 사이의 피드백 효과는 지역개발정책 입안자도 고려할 필요가 있다. 한 지역의 경제 성장이나 쇠퇴가 다른 지역에 어떤 영향을 미치는지 고려하여, 지역간 경제적 격차와 그것이 유발하는 사회경제적 문제를 예방할 필요가 있기 때문이다.